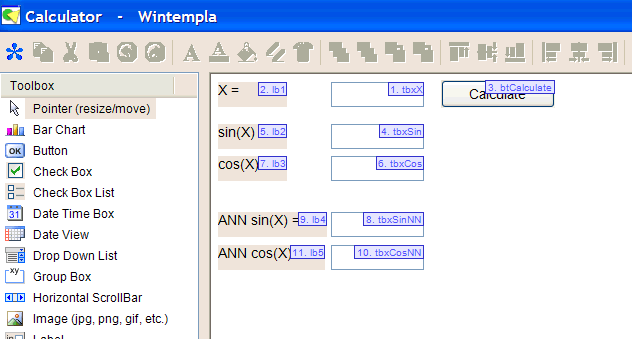
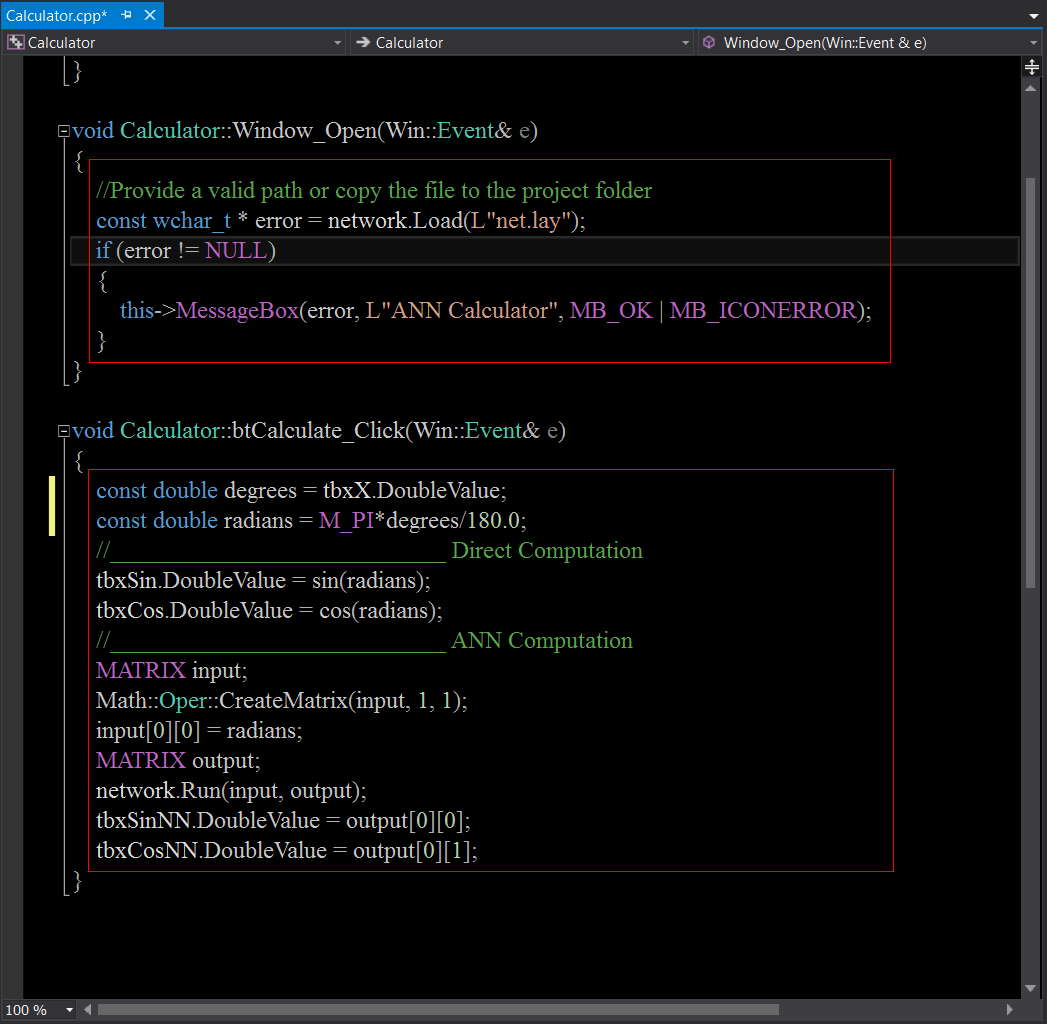
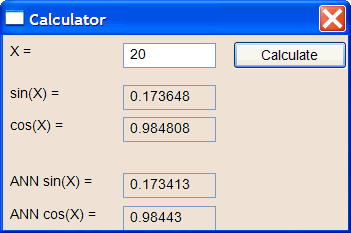
//________________________ Load and set the training set
Matrix trainSetInput;
trainSetInput.Load();
Matrix trainSetTarget;
trainSetTarget.Load();
//_______________________ Load the validation set
Matrix validSetInput;
validSetInput.Load();
Matrix validSetTarget;
validSetTarget.Load();
//________________________ Network setup
int numHidden = 1;
LayerNet net;
Matrix output;
Vector mseTraining;
mseTraining.Create(20);
Vector mseValidation;
mseValidation.Create(20);
for(numHidden = 0; numHidden < 20; numHidden++)
{
net.Create(1, numHidden, 0, 2);
net.SetInScaler(0, 0.0, 2.0*3.151927);
net.SetOutScaler(0, -1.0, 1.0);
net.SetOutScaler(1, -1.0, 1.0);
net.SetTrainSet(trainSetInput, trainSetTarget, false);
//
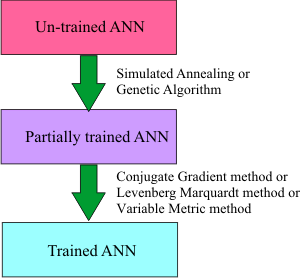
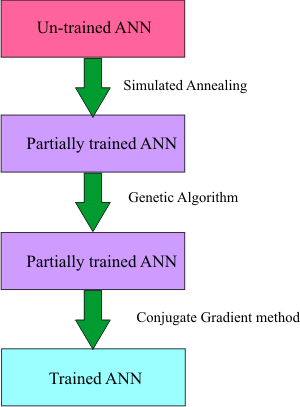
net.TrainSimAnneal(100, 100, 15, 0.01, false, 4, 1.0e-12);
//net.TrainGenetic(100, 100, 1.5, 0.01, 0.7, 1.0e-12);
//net.TrainLevenMar(1000,1.0e-12);
//_____________________________________________ check training
output = net.Run(trainSetInput);
mseTraining[numHidden] = ComputeMse(output, trainSetTarget);
//_____________________________________________ validation
output = net.Run(validSetInput);
mseValidation[numHidden] = ComputeMse(output, validSetTarget);
}
mseTraining.Save();
mseValidation.Save();
|
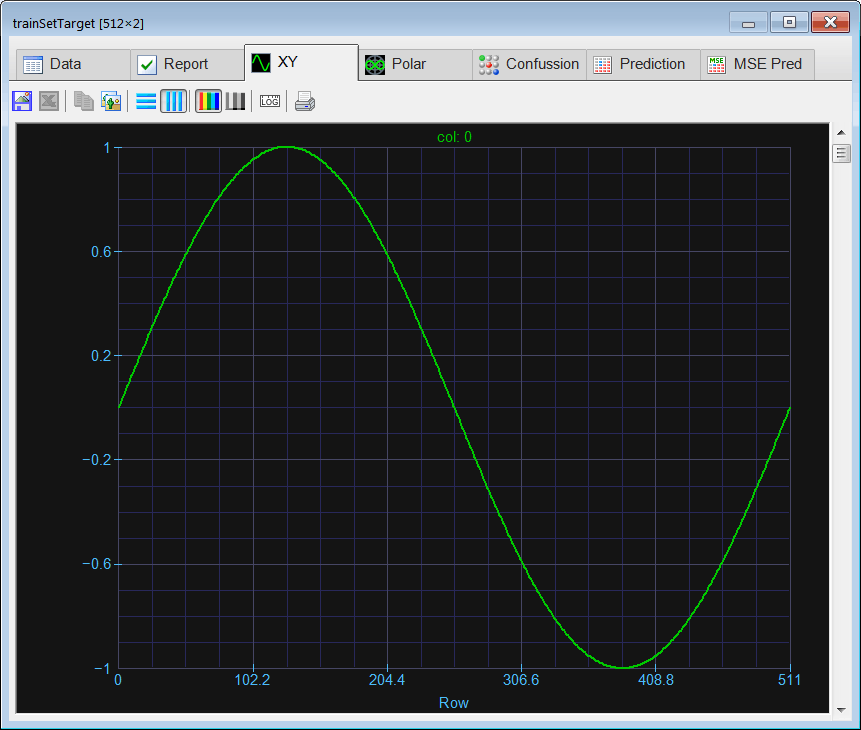
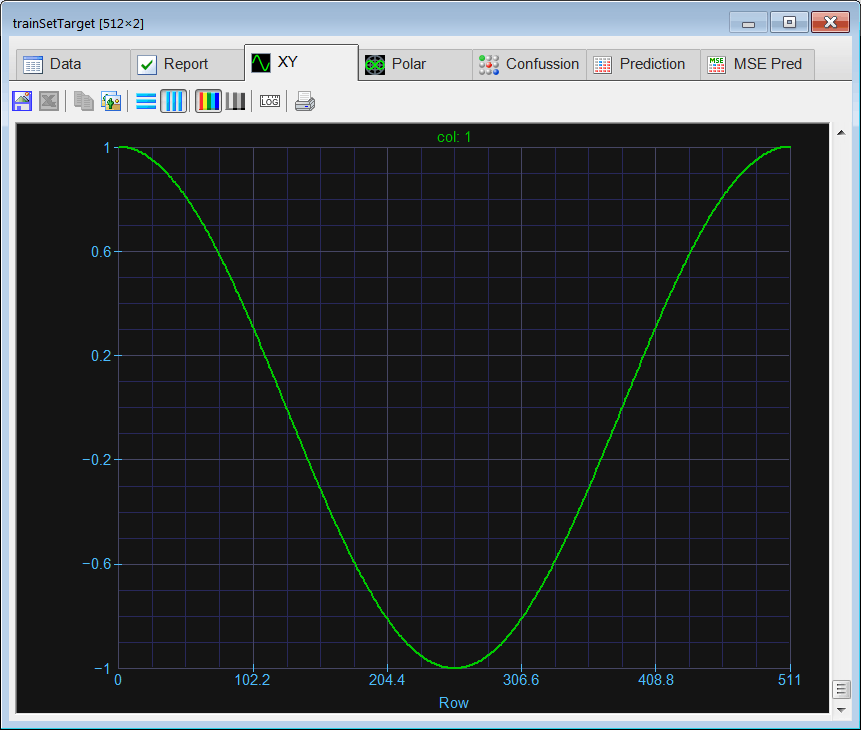
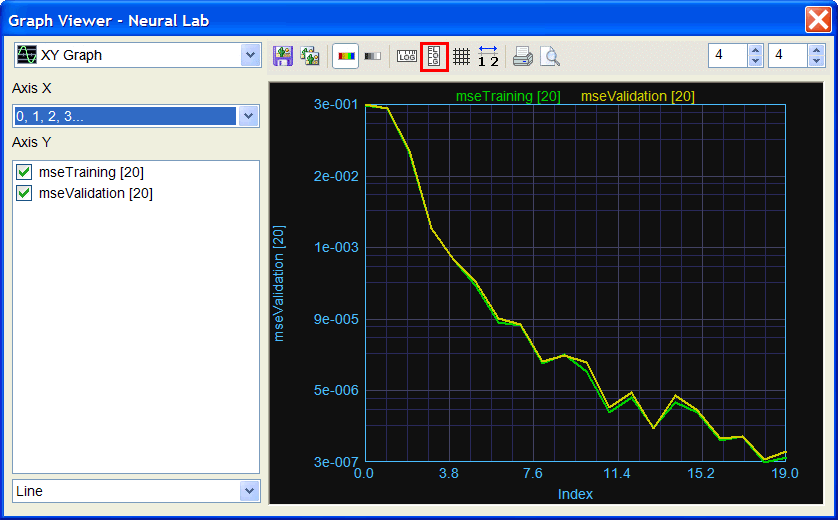
 Run click the button to execute the code. If you do not have any errors, the training set will be generated and displayed on the variable list and the file list.
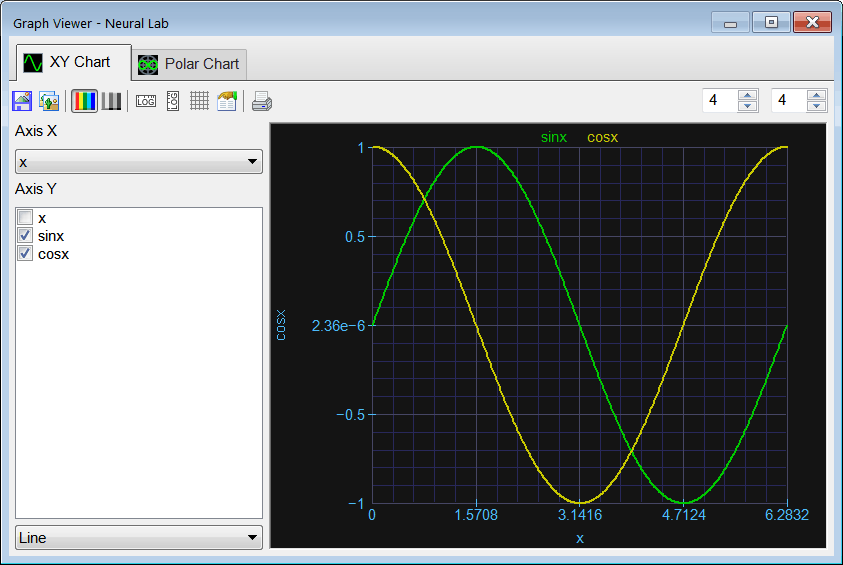
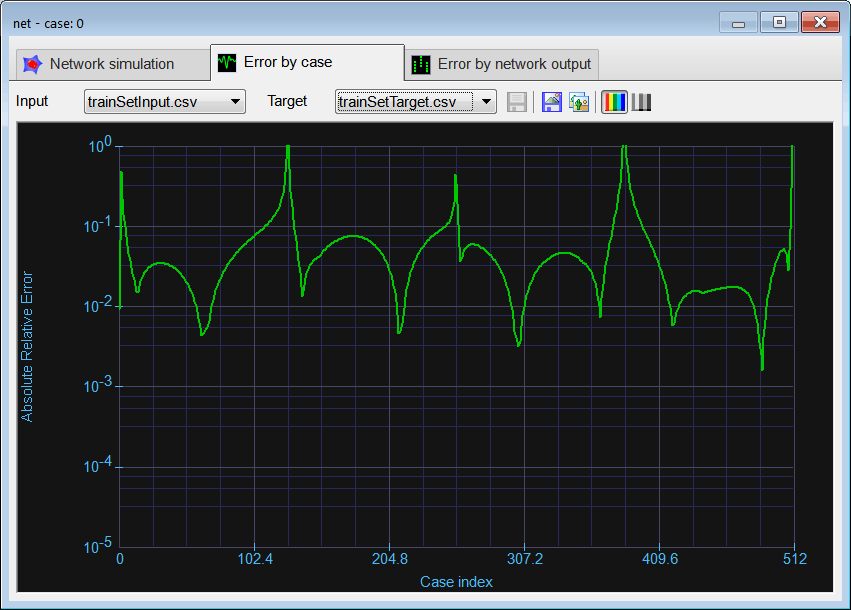
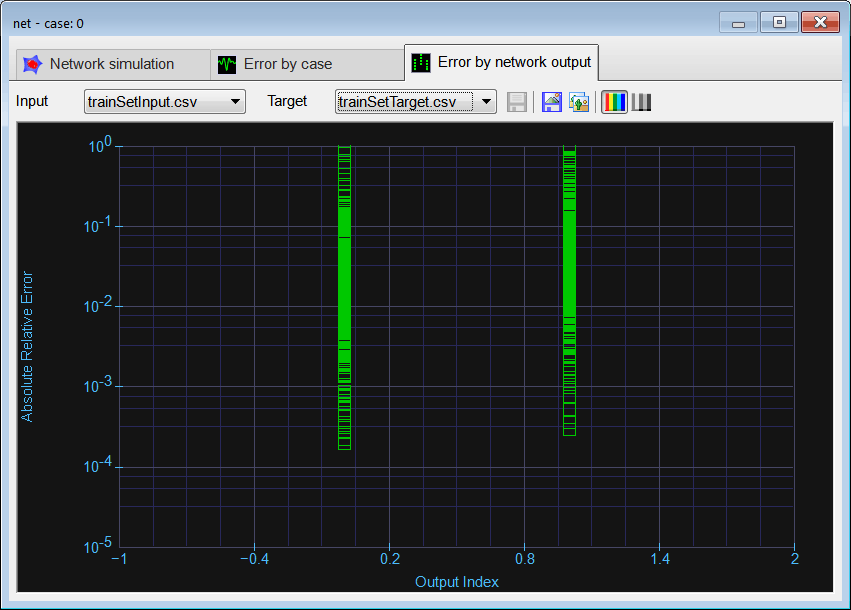
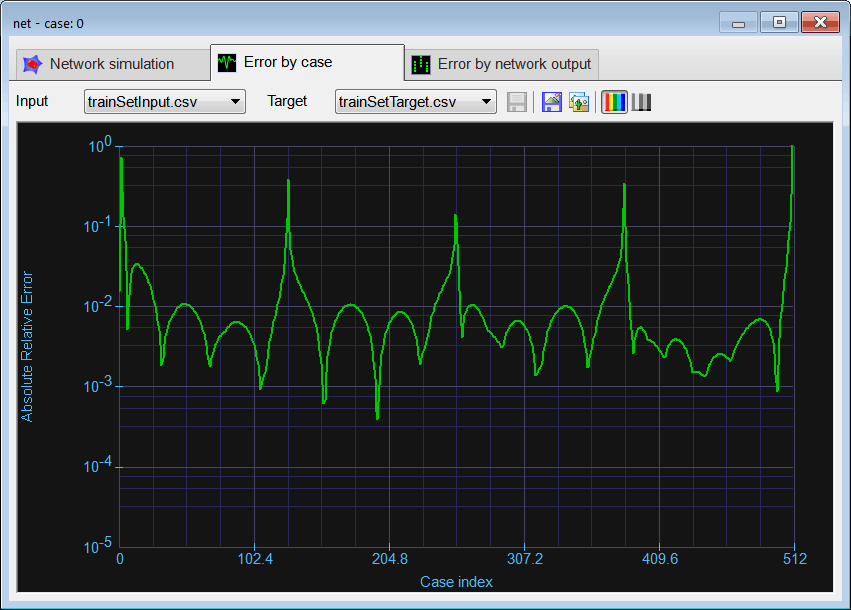
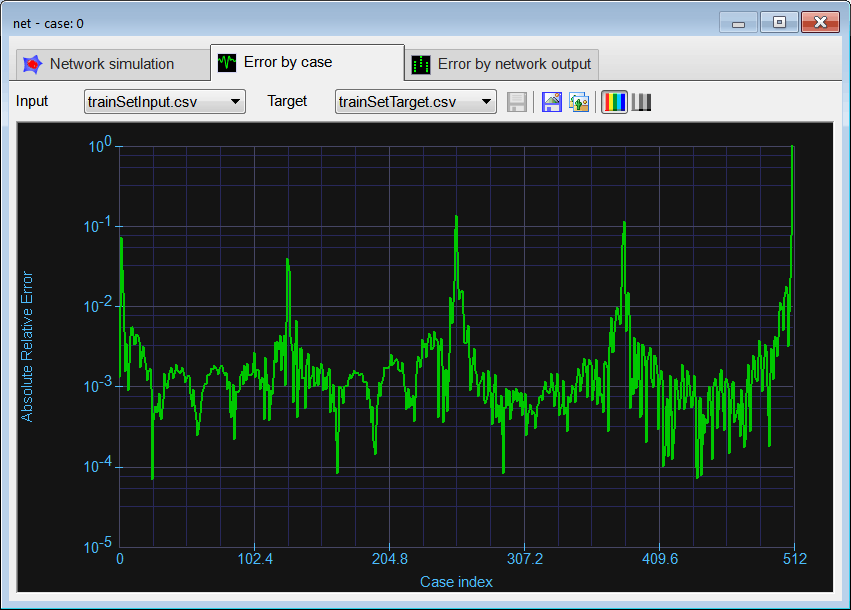
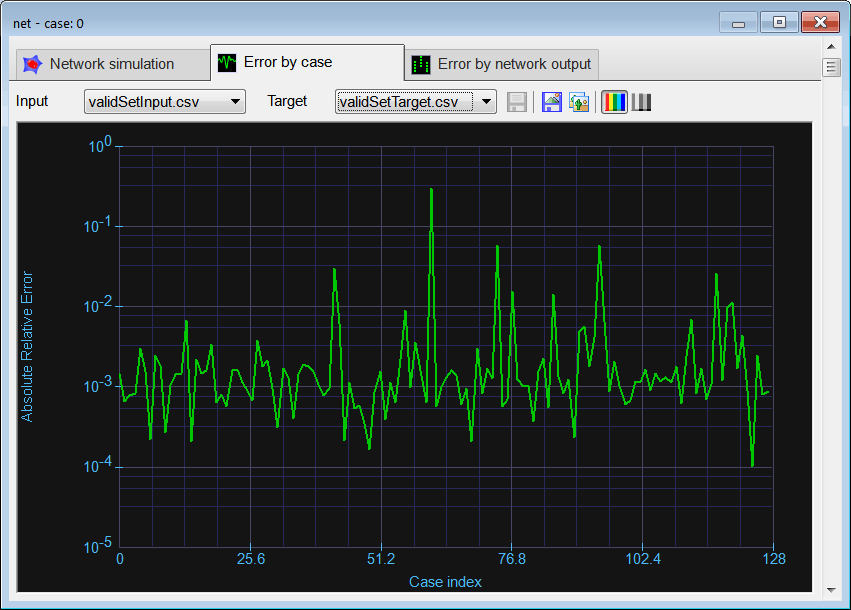
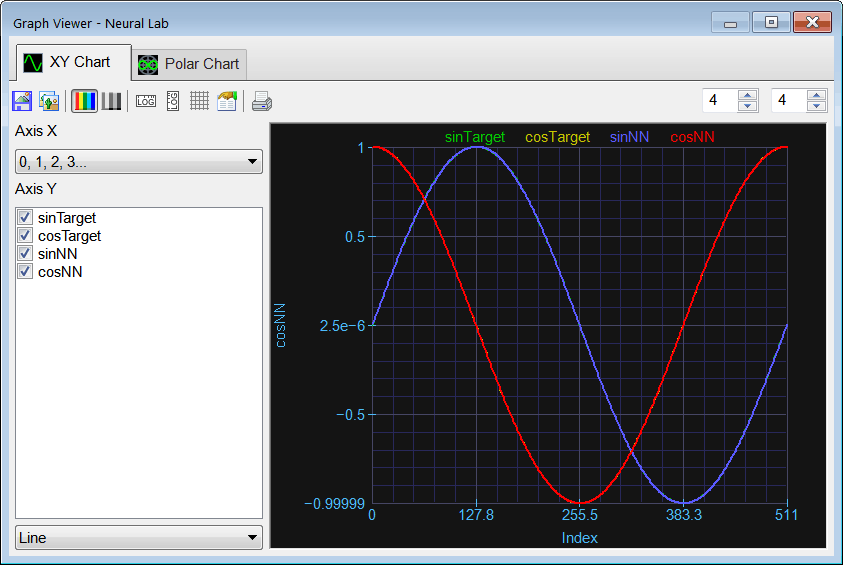
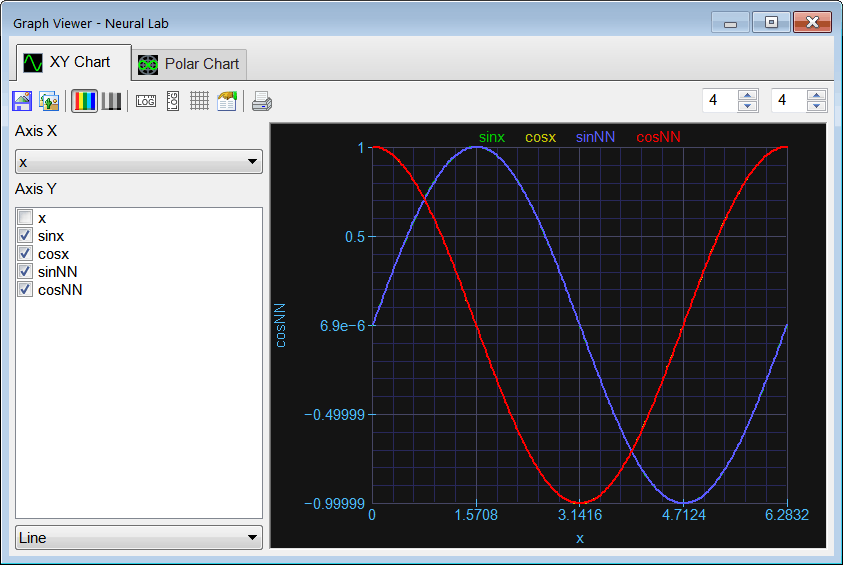
Run click the button to execute the code. If you do not have any errors, the training set will be generated and displayed on the variable list and the file list. Graph click the button to open the graph viewer and review the training set. Select the variables as shown.
Graph click the button to open the graph viewer and review the training set. Select the variables as shown.